NS3 SIMULATOR PROJECT TITLE
Tenor: A Measure of Central Tendency for Distributed Networks
We introduce a new tendency measure for a probability mass function (pmf) referred to as “tenor,” and defined in terms of the phase of the first non-zero frequency of the discrete Fourier transform of the pmf. This statistic is in the vicinity of the region of highest probability of the pmf. Unlike mean, tenor is robust against outliers, and unlike mode and median, tenor can be evaluated using only arithmetic operations of addition and multiplication, without the need for comparison operations.
We propose a distributed algorithm for computation of tenor in a graph and prove that for large networks represented by Erdos-Renyi graphs, [1] and by Watts-Strogatz graphs (small-world graphs), [2] the distributed algorithm converges. Numerical examples including the distributed computation of the majority vote are presented to demonstrate the operation of the algorithm.

 Click Here to watch our latest output video using NS3 simulator
Click Here to watch our latest output video using NS3 simulator 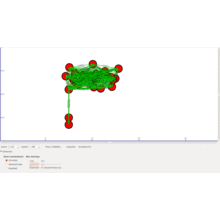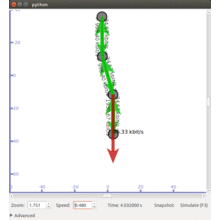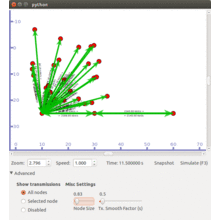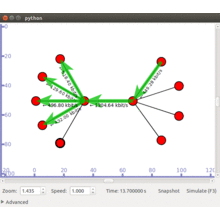 Click Here to watch our latest projects screenshots using NS3 simulator
Click Here to watch our latest projects screenshots using NS3 simulator