NS3 SIMULATOR PROJECT TITLE
Capacity Scaling of Wireless Social Networks
In this paper, we investigate capacity scaling laws of wireless social networks under the social-based session formation. We model a wireless social network as a three-layered structure, consisting of the physical layer, social layer, and session layer; and we introduce a cross-layer distance & density-aware model, called the population-based formation model, under which: 1) for each node vk, the number of its friends/followers, denoted by qk, follows a Zipf’s distribution with degree clustering exponent g; 2) qk anchor points are independently chosen according to a probability distribution with density function proportional to (Ek,X)-β, where Ek;X is the expected number of nodes (population) within the distance |vk-X| to vk, and β is the clustering exponent of friendship formation; 3) finally, qk nodes respectively nearest to those qk anchor points are selected as the friends of vk. We present the general density function of social relationship distribution, with general distribution of physical layer, serving as the basis for studying general capacity of wireless social networks.
As the first step of addressing this issue, for the homogeneous physical layer, we derive the social-broadcast capacity under both generalized physical and protocol interference models, taking into account general clustering exponents of both friendship degree and friendship formation in a 2-dimensional parameter space, i.e., (γ,β) ϵ[0,∞)2. Importantly, we notice that the adopted model with homogenous physical layer does not sufficiently reflect the advantages of the population-based formation model in terms of realistic validity and practicability. Accordingly, we introduce a random network model, called the center-clustering random model (CCRM) with node distribution exponent δ ϵ [0, &#- 221E;), highlighting the clustering and inhomogeneity property in real-life networks, and discuss how to further derive more generalnetwork capacity over 3-dimensional parameter space (δ,γ,β) ϵ [0, ∞)3 based on our results over (γ,β) ϵ [0, ∞)2.

 Click Here to watch our latest output video using NS3 simulator
Click Here to watch our latest output video using NS3 simulator 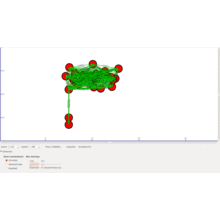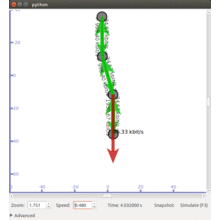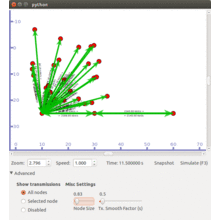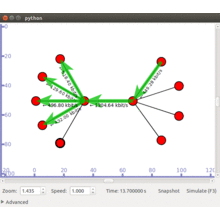 Click Here to watch our latest projects screenshots using NS3 simulator
Click Here to watch our latest projects screenshots using NS3 simulator